10 Analyzing the Meaning of Sentences (Extras)
10.1 Sets and Mathematical Functions
Sets
A set is a collection of entities, called the members of the set. Sets can be finite or infinite, or even empty. In Python, we can define a set just by listing its members; the notation is similar to specifying a list:
|
In mathematical notation, we would specify this set as:
| (1) | {'a', 'b', 1, 2, 3} |
Set membership is a relation — we can ask whether some entity x belongs to a set A (in mathematical notation, written x ∈ A).
|
However, sets differ from lists in that they are unordered collections. Two sets are equal if and only if they have exactly the same members:
|
The cardinality of a set A (written ∣A∣) is the number of members in A. We can get this value using the len() function:
|
The argument to the set() constructor can be any sequence, including a string, and just calling the constructor with no argument creates the empty set (written ∅).
|
We can construct new sets out of old ones. The union of two sets A and B (written A ∪ B) is the set of elements that belong to A or B. Union is represented in Python with |:
|
The intersection of two sets A and B (written A ∩ B) is the set of elements that belong to both A and B. Intersection is represented in Python with &. If the intersection of two sets is empty, they are said to be disjoint.
|
The (relative) complement of two sets A and B (written A − B) is the set of elements that belong to A but not B. Complement is represented in Python with -.
|
So far, we have described how to define 'basic' sets and how to form new sets out of those basic ones. All the basic sets have been specified by listing all their members. Often we want to specify set membership more succinctly:
| (2) | the set of positive integers less than 10 |
| (3) | the set of people in Melbourne with red hair |
We can informally write these sets using the following predicate notation:
| (4) | {x | x is a positive integer less than 10} |
| (5) | {x | x is a person in Melbourne with red hair} |
In axiomatic set theory, the axiom schema of comprehension states that given a one-place predicate P, there is set A such that for all x, x belongs to A if and only if (written ≡) P(x) is true:
| (6) | ∃A∀x.(x ∈ A ≡ P(x)) |
From a computational point of view, (6) is problematic: we have to treat sets as finite objects in the computer, but there is nothing to stop us defining infinite sets using comprehension. Now, there is a variant of (6), called the axiom of restricted comprehension, that allows us to specify a set A with a predicate P so long as we only consider xs which belong to some already defined set B:
| (7) | ∀B ∃A∀x. (x ∈ A ≡ x ∈ B ∧ P(x)) |
(For all sets B there is a set A such that for all x, x belongs to A if and only if x belongs to B and P(x) is true.) This is equivalent to the following set in predicate notation:
| (8) | {x | x ∈ B ∧ P(x)) |
(7) corresponds pretty much to what we get with list comprehension in Python: if you already have a list, then you can define a new list in terms of the old one, using an if condition. In other words, (9) is the Python counterpart of (7).
| (9) | set([x for x in B if P(x)]) |
To illustrate this further, the following list comprehension relies on the existence of the previously defined set nats (n % 2 is the remainder when n is divided by 2):
|
Now, when we defined evens before, what we actually had was a set of strings, rather than Python integers. But we can use int to coerce the strings to be of the right type:
|
If every member of A is also a member of B, we say that A is a subset of B (written A ⊆ B). The subset relation is represented in Python with <=.
|
As the above examples show, B can contain more members than A for A ⊆ B to hold, but this need not be so. Every set is a subset of itself. To exclude the case where a set is a subset of itself, we use the relation proper subset (written A ⊂ B). In Python, this relation is represented as <.
|
Sets can contain other sets. For instance, the set A = {{a}, {b} } contains the two singleton sets {a} and {b}. Note that {a} ⊆ A does not hold, since a belongs to {a} but not to A. In Python, it is a bit more awkward to specify sets whose members are also sets; the latter have to be defined as frozensets, i.e., immutable objects.
|
We also need to be careful to distinguish between the empty set ∅ and the set whose only member is the empty set: {∅}.
Tuples
We write 〈x1, …, xn〉 for the ordered n-tuple of objects x1, …, xn, where n ≥ 0. These are exactly the same as Python tuples. Two tuples are equal only if they have the same lengths, and the same objects in the same order.
|
A tuple with just 2 elements is called an ordered pair, with just three elements, an ordered triple, and so on.
Given two sets A and B, we can form a set of ordered pairs by drawing the first member of the pair from A and the second from B. The Cartesian product of A and B, written A × B, is the set of all such pairs. More generally, we have for any sets S1, …, Sn,
| (10) | S1 × … × Sn = {〈x1, …, xn〉 ∣ xi ∈ Si} |
In Python, we can build Cartesian products using list comprehension. As you can see, the sets in a Cartesian product don't have to be distinct.
|
Relations and Functions
In general, a relation R is a set of tuples. For example, in set-theoretic terms, the binary relation kiss is the set of all ordered pairs 〈x, y〉 such that x kisses y. More formally, an n-ary relation over sets S1, …, Sn is any set R ⊆ S1 × … × Sn.
Given a binary relation R over two sets A and B, not everything in A need stand in the R relation to something in B. As an illustration, consider the set evens and the relation mod defined as follows:
|
Now, mod ⊆ evens × evens, but there are elements of evens, namely 6, 8 and 10, that do not stand in the mod relation to anything else in evens. In this case, we say that only 2 and 4 are in the domain of the mod relation. More formally, for a relation R over A × B, we define
| (11) | dom(R) = {x ∣ ∃y.〈x, y〉 ∈ A × B} |
Correspondingly, the set of entities in B which are the second member of a pair in R is called the range of R, written ran(R).
We can visually represent the relation mod by drawing arrows to indicate elements that stand in the relation, as shown in 10.1.
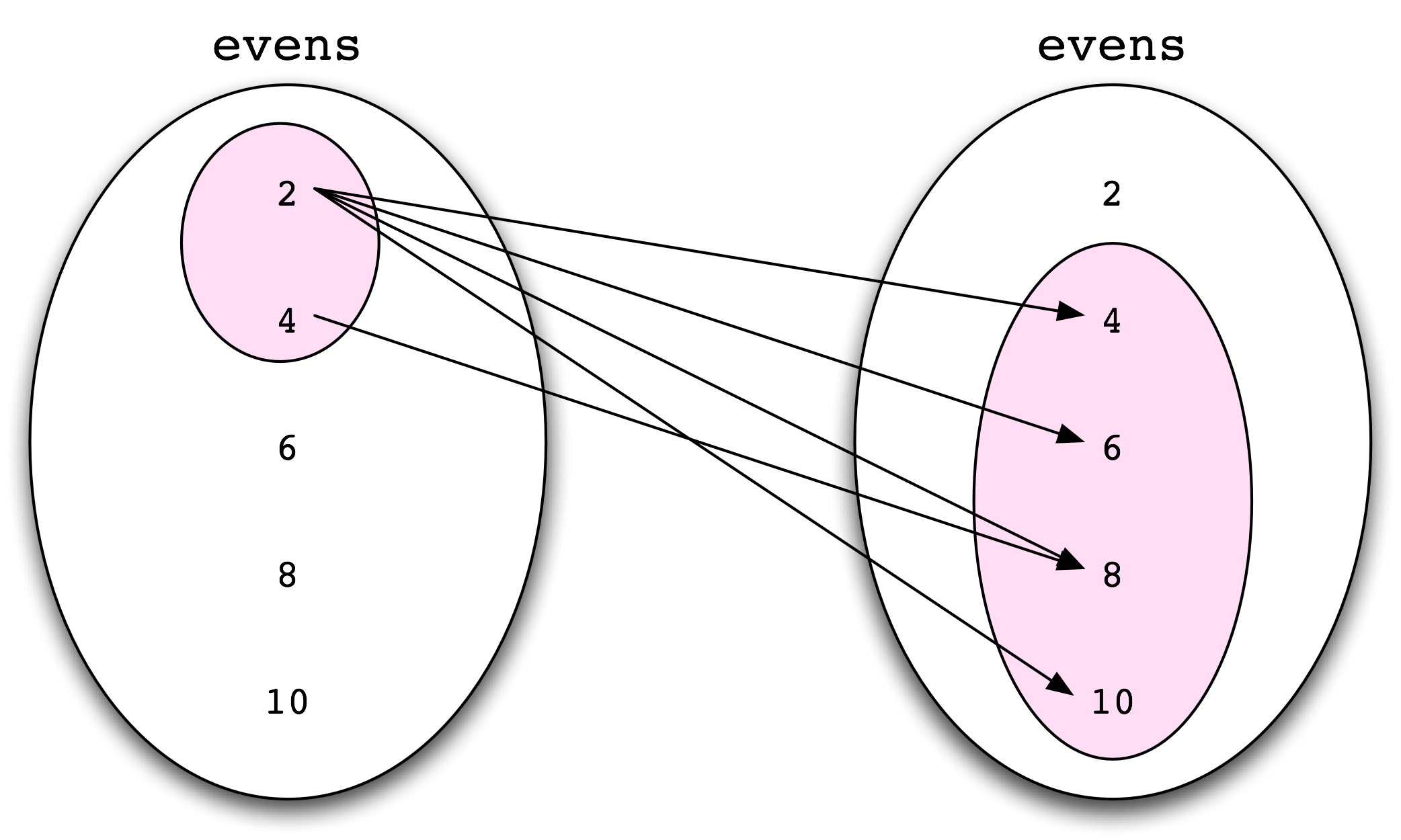
Figure 10.1: Visual Representation of a Relation
The domain and range of the relation are shown as shaded areas in 10.1.
A relation R ⊆ A × B is a (set-theoretic) function just in case it meets the following two conditions:
- For every a ∈ A there is at most one b ∈ B such that 〈a, b〉.
- The domain of R is equal to A.
Thus, the mod relation defined earlier is not a function, since the element 2 is paired with four items, not just one. By contrast, the relation doubles defined as follows is a function:
|
If f is a function ⊆ A × B, then we also say that f is a function from A to B. We also write this as f: A → B. If 〈x, y〉 ∈ f, then we write f(x) = y. Here, x is called an argument of f and y is a value. In such a case, we may also say that f maps x to y.
Given that functions always map a given argument to a single value, we can also represent them in Python using dictionaries (which incidentally are also known as mapping objects). The update() method on dictionaries can take as input any iterable of key/value pairs, including sets of two-membered tuples:
|
A function f: S1 × … × Sn → T is called an n-ary function; we usually write f(s1, …, sn) rather than f(〈s1, …, sn〉). For sets A and B, we write AB for the set of all functions from A to B, that is {f ∣ f: A → B}. If S is a set, then we can define a corresponding function fS called the characteristic function of S, defined as follows:
| (12) | fS(x) = True if x ∈ S
fS(x) = False if x ∉ S
|
fS is a member of the set {True, False}S.
It can happen that a relation meets condition (1) above but fails condition (2); such relations are called partial functions. For instance, let's slightly modify the definition of doubles:
|
doubles2 is a partial function since its domain is a proper subset of evens. In such a case, we say that doubles2 is defined for 2 and 4 but undefined for the other elements in evens.
Exercises
☼ For each of the following sets, write a specification by hand in predicate notation, and an implementation in Python using list comprehension.
- {2, 4, 8, 16, 32, 64}
- {2, 3, 5, 7, 11, 13, 17}
- {0, 2, -2, 4, -4, 6, -6, 8, -8}
☼ The powerset of a set A (written ℘A) is the set of all subsets of A, including the empty set. List the members of the following sets:
- ℘{a, b, c}:
- ℘{a}
- ℘{∅}
- ℘∅
◑ Write a Python function to compute the powerset of an arbitrary set. Remember that you will have to use frozenset for this.
☼ Consider the relation doubles, where evens is defined as in the text earlier:
>>> doubles = set([(m,m*2) for m in evens])
Is doubles a relation over evens? Explain your answer.
◑ What happens if you try to update a dictionary with a relation that is not a function?
☼ Write a couple of Python functions that, for any set of pairs R, return the domain and range of R.
◑ Let S be a family of three children, {Bart, Lisa, Maggie}. Define relations R ⊆ S × S such that:
- dom(R) ⊂ S;
- dom(R) = S;
- ran(R) = S;
- ran(R) = S;
- R is a total function on S.
- R is a partial function on S.
◑ Write a Python function that, for any set of pairs R, returns True if and only if R is a function.
About this document...
This is a chapter from Natural Language Processing with Python, by Steven Bird, Ewan Klein and Edward Loper, Copyright © 2009 the authors. It is distributed with the Natural Language Toolkit [http://www.nltk.org/], Version 2.0.1rc1, under the terms of the Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License [http://creativecommons.org/licenses/by-nc-nd/3.0/us/].
This document was built on Mon 15 Oct 2012 16:46:09 EST